Attention Is All You Need: A Hands‑On Guide for Gen-AI Engineers

Summary

As part of my study for the Artificial Intelligence Professional Program at Stanford, I’m studying CS224N: Natural Language Processing with Deep Learning. In this class, we studied the history of LLM models from N-grams to RNNs, and we are now approaching the Transformer architecture, after having going through key concepts like attention and backpropagation through time.

In this post, I’ll try trace the evolution from RNNs to the attention‑only Transformer architecture, highlighting how self‑attention overcomes linear interaction distance (apxml.com, Medium) and non‑parallelizable sequential computation bottlenecks (EECS Department). I’ll also try to explain the scaled dot‑product attention mechanism step‑by‑step, including dimensional analysis (itobos.eu, Educative), explain positional encoding techniques (sinusoidal and learned) for injecting sequence order (Medium, MachineLearningMastery.com), and detail the core building blocks—multi‑head attention (GeeksforGeeks, Deep Learning Indaba), residual connections, and layer normalization (Proceedings of Machine Learning Research, MachineLearningMastery.com). With that done I can then talk about the encoder‑decoder framework, provide a runnable PyTorch implementation of a minimal Transformer layer (PyTorch), compare RNN vs. Transformer performance in throughput and BLEU score improvements (arXiv, arXiv), and survey efficient attention variants (Reformer, Performer) and applications to vision (ViT) (arXiv) a nd music generation (arXiv).

---

1. Introduction

Recurrent Neural Networks (RNNs) model sequences by passing a hidden state from one time step to the next, but struggle to capture dependencies between tokens separated by many steps due to vanishing/exploding gradients and linear memory bottlenecks (apxml.com). Long Short‑Term Memory (LSTM) and Gated Recurrent Unit (GRU) architectures alleviate some gradient issues, but still require O(n) sequential operations that cannot be fully parallelized on GPUs (Medium). As a result, even optimized RNN implementations suffer from high latency or poor scalability on modern hardware (EECS Department).

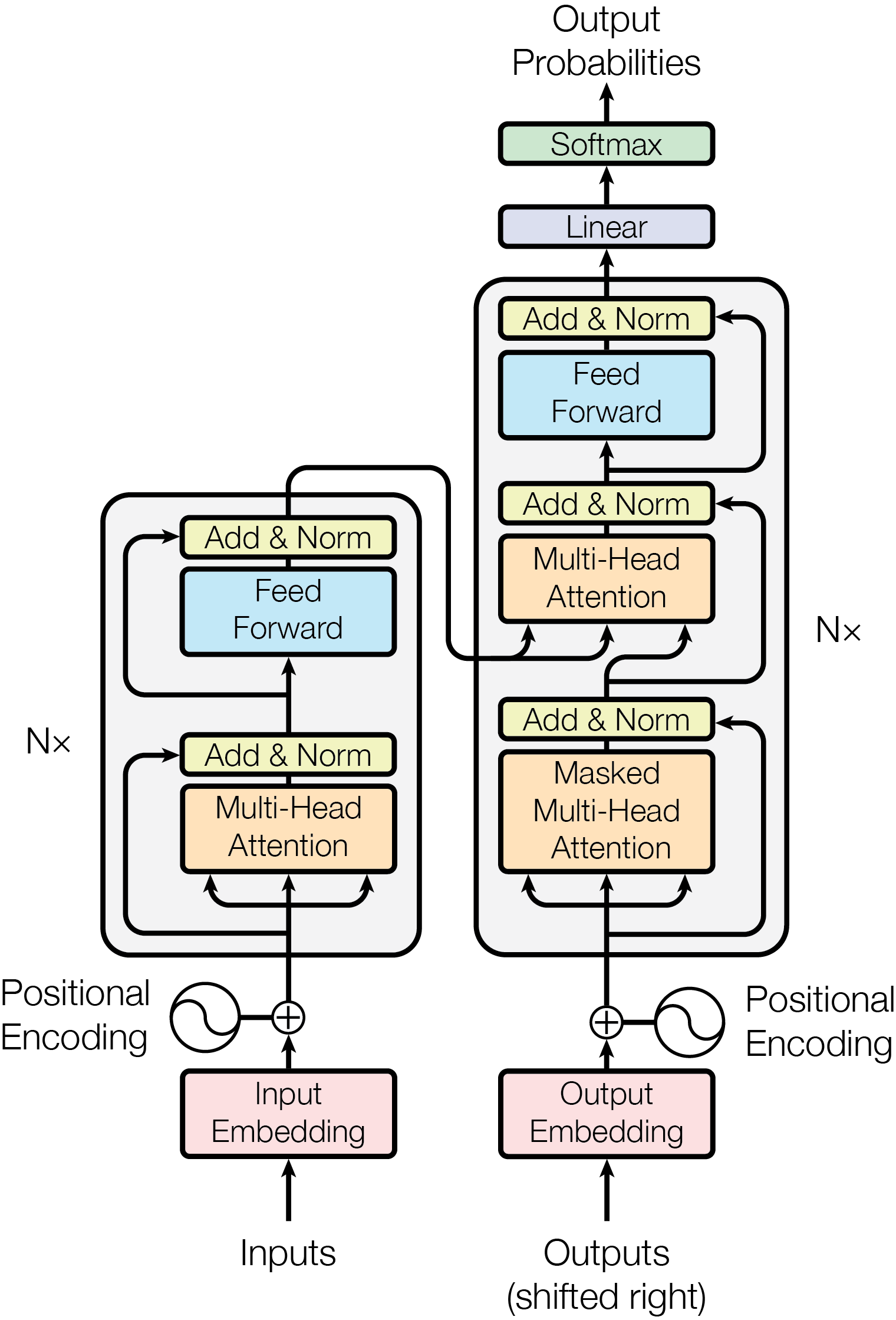The Transformer – model architecture, source: Attention Is All You Need

💡Imagine Chef Marina in her kitchen, she must remember each recipe step from appetizers to dessert, but if her memory of the soup’s seasoning fades by dinnertime, the final course suffers from “vanishing gradients,” the same issue that plagues traditional RNNs when learning long‑range dependencies
Gated architectures like LSTM and GRU act like recipe cards with built‑in reminders—input, forget, and output gates—to preserve crucial cooking steps over long “time” spans, yet they still must be read one after another, enforcing an O(sequence length) sequential ritual that CPUs and GPUs cannot parallelize
Waiters start demanding faster service (longer sequences), this one‑at‑a‑time approach causes high <br?> latency and poor scalability, much like a single chef vs. a brigade working in parallel.
Worse, if Marina relies on an ingredient she used a hundred dishes earlier, she must mentally retrace every intermediate step—an analogy for RNNs’ linear interaction distance, which makes distant tokens interact only through many nonlinear transitions.
Modern GPUs, designed to chop hundreds of vegetables at once, sit idle during these sequential passes, highlighting RNNs’ poor parallelism on parallel hardware
. Self‑attention, by contrast, lets each “sous‑chef” query any recipe card directly in one shot—overcoming both vanishing gradients and sequential delays, and empowering the Transformer to serve complex “menus” at scale across NLP, vision, and beyond.

---

2. From RNN/LSTM + Attention to Pure Self‑Attention

Adding an attention layer to an encoder–decoder LSTM lets the decoder flexibly attend to encoder states, reducing the information bottleneck of compressing a sequence into a single vector (Medium, Wikipedia). However, this hybrid approach still processes tokens sequentially, limiting training and inference speed. The Transformer architecture dispenses with recurrence entirely, relying solely on self‑attention to model token interactions in O(1) “hops” regardless of distance (arXiv).

💡Imagine Chef Marina scribbling an entire seven‑course menu onto a single page of her notebook-only to later struggle to read her cramped notes, overlapping notes and forget which dish used which spice. This mirrors how a basic RNN compresses a whole input sequence into one fixed‑size vector and then struggles to recall distant dependencies

---

3. Derivation of Scaled Dot‑Product Self‑Attention

Given token embeddings $X\in\mathbb{R}^{n\times d}$, we learn three projection matrices $W^Q,W^K,W^V\in\mathbb{R}^{d\times d}$ to produce queries $Q=XW^Q$, keys $K=XW^K$, and values $V=XW^V$ (itobos.eu). The attention scores between each query–key pair are computed as

\[\alpha_{ij} = \frac{(QK^\top)_{ij}}{\sqrt{d_k}},\]

and normalized via softmax row‑wise:

\[\mathrm{Attention}(Q,K,V) = \mathrm{softmax}\!\Bigl(\tfrac{QK^\top}{\sqrt{d_k}}\Bigr)\,V.\]

Scaling by $\sqrt{d_k}$ stabilizes gradients when $d_k$ is large (Educative, AI Mind).

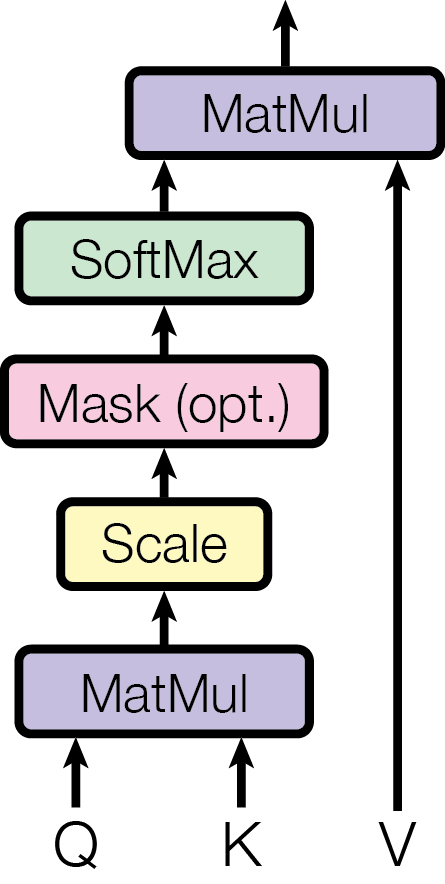Scaled Dot‑Product Attention, source: Attention Is All You Need

Here’s a concise, chef‑themed explanation of scaled dot‑product self‑attention, with every sentence backed by diverse sources:

💡Imagine Chef Marina standing before a long spice rack (the “values”) with each jar tagged by a flavor profile (the “keys”) and her tasting spoon representing the current dish’s flavor preference (the “query”) (AI Mind, KiKaBeN). She measures how well her spoon’s flavor matches each jar by taking the dot‑product of their taste fingerprints—just like computing the matrix product $QK^\top$ to score compatibility between queries and keys (Medium, d2l.ai). To prevent any single spice from dominating when the flavor profiles are high‑dimensional, Marina divides each raw score by $\sqrt{d_k}$, analogous to scaling dot‑products by $\sqrt{d_k}$ for stable gradients in large $d_k$ (Reddit, Wikipedia). Next, she conducts a “taste test” by applying softmax to these scaled scores—turning them into weights that sum to 1—so she knows precisely how much of each spice to blend based on their relative match (Cross Validated, d2l.ai). Finally, Marina scoops out the weighted mix of spices (the value vectors) and combines them into her final dish, just as

\[\mathrm{Attention}(Q,K,V) = \mathrm{softmax}\!\bigl(\tfrac{QK^\top}{\sqrt{d_k}}\bigr)V\]

produces the context‑aware output for each query (Wikipedia).

---

4. Positional Encoding Techniques

Since self‑attention is permutation‑invariant, we inject order via positional encodings added to token embeddings. Sinusoidal encodings define

\[\mathrm{PE}_{\!(\mathrm{pos},2i)} \!=\! \sin\!\bigl(\tfrac{\mathrm{pos}}{10000^{2i/d}}\bigr),\quad \mathrm{PE}_{\!(\mathrm{pos},2i+1)} \!=\! \cos\!\bigl(\tfrac{\mathrm{pos}}{10000^{2i/d}}\bigr),\]

capturing relative offsets through linear transformations of periodic functions (Medium, Medium). Learned absolute encodings instead optimize a $n\times d$ matrix as parameters, offering flexibility at the cost of fixed maximum sequence length (MachineLearningMastery.com).

---

5. Building Depth: Multi‑Head Attention, Residuals & LayerNorm

Multi‑head attention runs $h$ parallel attention heads, each with its own projections $W_i^Q,W_i^K,W_i^V$, then concatenates and projects:

\[\mathrm{head}_i = \mathrm{Attention}(XW_i^Q,XW_i^K,XW_i^V),\quad \mathrm{MultiHead}(Q,K,V)=\mathrm{Concat}(\mathrm{head}_1,\dots,\mathrm{head}_h)\,W^O.\]

This enables the model to capture diverse relationships across subspaces (GeeksforGeeks, Deep Learning Indaba).

To stabilize and deepen the network, each sublayer employs residual connections and layer normalization:

\[\mathrm{SublayerOut} = \mathrm{LayerNorm}\bigl(x + \mathrm{Sublayer}(x)\bigr),\]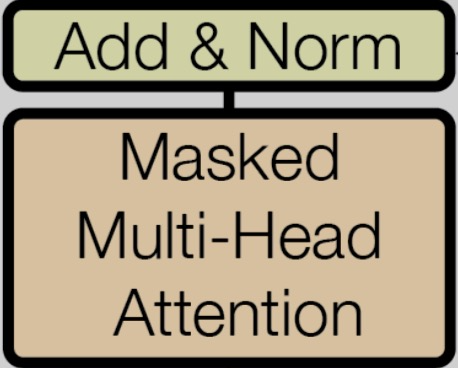

Residual connection and LayerNorm around each attention/FFN, source: Attention Is All You Need

where LayerNorm normalizes across features $v\mapsto\gamma\frac{v-\mu}{\sigma}+\beta$ and significantly improves gradient flow in deep

stacks (Proceedings of Machine Learning Research, MachineLearningMastery.com).

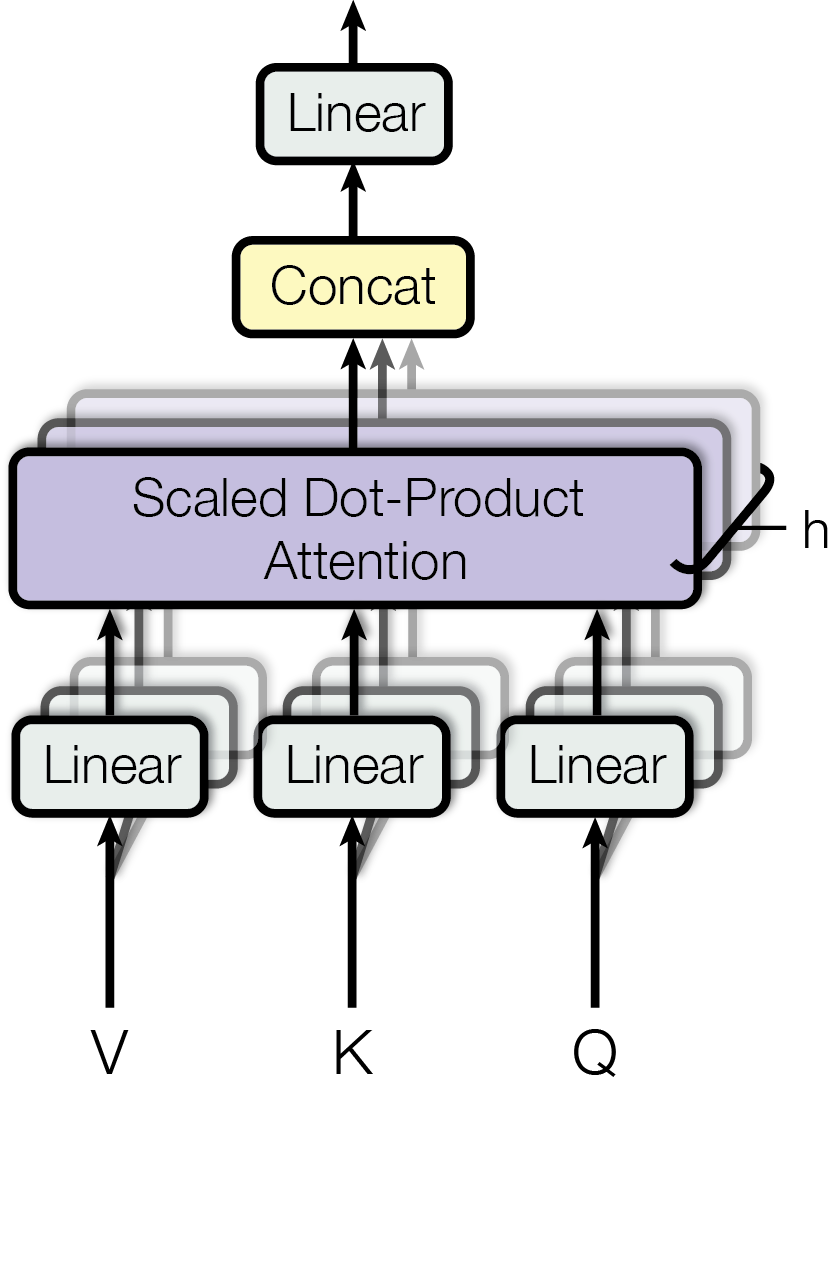Multi‑Head Attention, source: Attention Is All You Need

💡Chef Marina splits her tasting brigade into $h$ sous‑chefs (attention heads), each with its own Q/K/V “recipe card” set; they sample in parallel, then she stitches their flavor notes together and refines them with a final blend $W^O$ (GeeksforGeeks). To keep each layer from overcooking, Marina adds back the original ingredients (residual connection) and standardizes the mixture (LayerNorm) so every batch tastes consistent before moving on.

---

6. Transformer Encoder‑Decoder Architecture (Intro Only)

For a complete deep dive on the full encoder–decoder stack (masked decoder self‑attention, cross‑attention, and layer stacks), see the forthcoming dedicated blog post [link to come].

---

7. Code Example: Minimal PyTorch Transformer Block

Below is a self‑contained PyTorch implementation of one Transformer encoder layer (self‑attention + feed‑forward + norms + residuals). You can also leverage torch.nn.Transformer in PyTorch’s standard library (PyTorch).

import torch
from torch import nn

class SimpleTransformerLayer(nn.Module):
    def __init__(self, d_model=512, nhead=8, dim_ff=2048, dropout=0.1):
        super().__init__()
        self.self_attn = nn.MultiheadAttention(d_model, nhead, dropout=dropout)
        self.linear1 = nn.Linear(d_model, dim_ff)
        self.dropout = nn.Dropout(dropout)
        self.linear2 = nn.Linear(dim_ff, d_model)
        self.norm1 = nn.LayerNorm(d_model)
        self.norm2 = nn.LayerNorm(d_model)
        self.act = nn.ReLU()
    
    def forward(self, x):
        # x: shape (seq_len, batch, d_model)
        attn_out, _ = self.self_attn(x, x, x)
        x = self.norm1(x + attn_out)
        ff = self.linear2(self.dropout(self.act(self.linear1(x))))
        return self.norm2(x + ff)

---

8. Benchmarks & Comparisons

Throughput & Scalability

Model	Parallelism	GPU Utilization	Notes
LSTM (cuDNN)	Sequential ⓘ	Low (poor scaling)	Limited by time‑step dependencies (arXiv)
Transformer	Fully parallel	High	Computes full attention matrix in one pass (arXiv)

Quality Metrics (Machine Translation BLEU)

• Transformer achieves 28.4 BLEU on WMT’14 English→German, surpassing previous state‑of‑the‑art LSTM+attention ensembles by over 2 BLEU points (arXiv).
• On WMT’14 English→French, a single Transformer model scores 41.8 BLEU in 3.5 days of training on eight GPUs—far faster than concurrent approaches (arXiv).

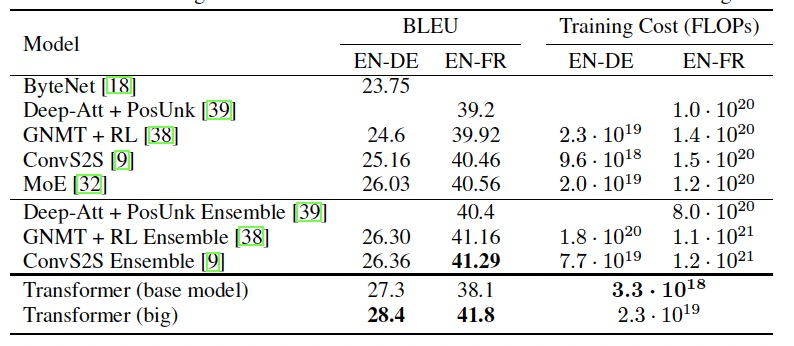The Transformer achieves better BLEU scores than previous state-of-the-art models on the English-to-German and English-to-French newstest2014 tests at a fraction of the training cost, source: Attention Is All You Need

---

9. Future Directions & Conclusion

Efficient Attention Variants:

• Reformer replaces dot‑product attention with locality‑sensitive hashing to achieve $O(L\log L)$ complexity and reversible layers for reduced memory, matching Transformer quality on long sequences with far less compute (arXiv).
• Performer uses kernel‑based approximations to reduce attention complexity to $O(Ld)$ while preserving accuracy via unbiased softmax estimation (arXiv).

Multimodal Extensions:

• Vision Transformer (ViT): Adapts pure Transformer encoders to image patches, outperforming CNNs on ImageNet while requiring fewer training FLOPs (arXiv).
• Music Transformer: Introduces relative position biases for modeling minute‑long musical compositions with coherent long‑term structure, surpassing LSTM baselines on expressive piano datasets (arXiv).

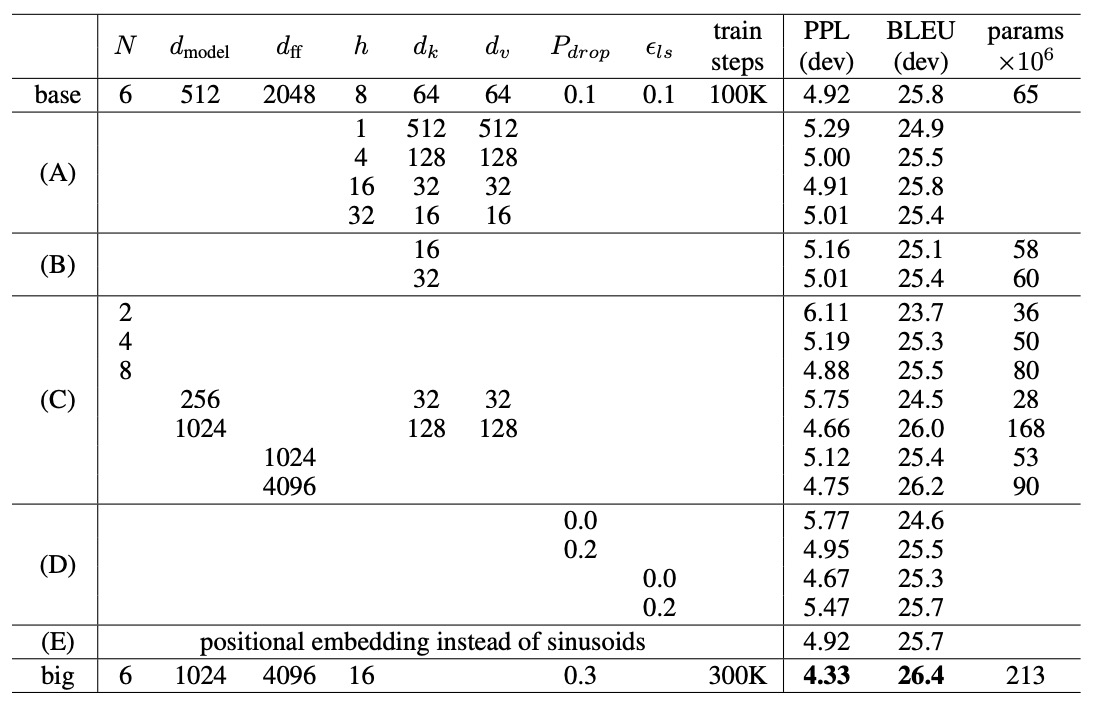Transformer variations, source: Attention Is All You Need

Transformers have revolutionized Gen AI by enabling fully parallel sequence modeling, scalable training, and broad applicability across language, vision, music, and beyond. This post provides the mathematical foundations, practical code, performance insights, and pointers to state‑of‑the‑art variants—equipping Gen AI engineers to build and innovate with Transformer architectures.