Beyond the Thought Vector: The Evolution of Attention in Deep Learning
Sequence-to-sequence (seq2seq) models without attention compress an entire source sentence into a single fixed-length vector, then feed that into a decoder to produce the target sentence. While this “thought vector” approach works for short inputs, it struggles as sentence lengths grow: cramming all semantic, syntactic, and contextual information into one vector creates a severe information bottleneck (arxiv.org, en.wikipedia.org).
From Bahdanau, Cho & Bengio (2014), Neural Machine Translation by Jointly Learning to Align and Translate
Humans, by contrast, don’t translate by memorizing an entire sentence before beginning; we glance back at specific words or phrases as we generate each target word. Attention emulates this behavior in neural networks, allowing the decoder to dynamically focus on different parts of the source as needed (distill.pub).
The Original (Additive) Attention Mechanism
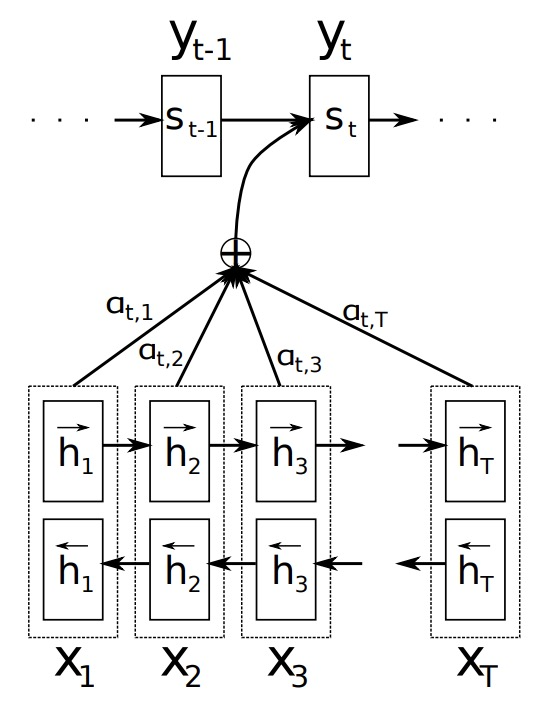
Dzmitry Bahdanau, Kyunghyun Cho, and Yoshua Bengio (2014) introduced the first “soft” attention in neural machine translation. Instead of forcing the decoder to rely solely on the final encoder state, they let it score each encoder hidden state $h_i$ against the current decoder state $s_{t-1}$:
\[e_{t,i} = v_a^\top \,\tanh\bigl(W_1\,s_{t-1} + W_2\,h_i\bigr) \quad,\quad \alpha_{t,i} = \frac{\exp(e_{t,i})}{\sum_j \exp(e_{t,j})} \quad,\quad c_t = \sum_i \alpha_{t,i}\,h_i\]Here, $\alpha_{t,i}$ are attention weights that form a probability distribution over source positions. The context vector $c_t$ is their weighted sum, which the decoder then uses (via concatenation or addition) to predict the next word (arxiv.org).
From Bahdanau, Cho & Bengio (2014), Neural Machine Translation by Jointly Learning to Align and Translate
Multiplicative (Dot-Product) & Bilinear Attention
Luong, Pham, and Manning (2015) proposed two simpler variants:
Dot-product attention
\[e_{t,i} = s_{t-1}^\top\,h_i\]General (bilinear) attention
\[e_{t,i} = s_{t-1}^\top\,W\,h_i\]
Dot-product is fast and parameter-free, but requires $s$ and $h$ to share dimensionality. The bilinear form introduces a learned matrix $W$, allowing the model to map between different subspaces and to emphasize which components of $s$ and $h$ should interact (arxiv.org).
To reduce $W$’s parameter count, one can factor it into two low-rank matrices (i.e., projections into a lower-dimensional space before dot-product), an idea that underpins the scaled dot-product attention in Transformers (next).
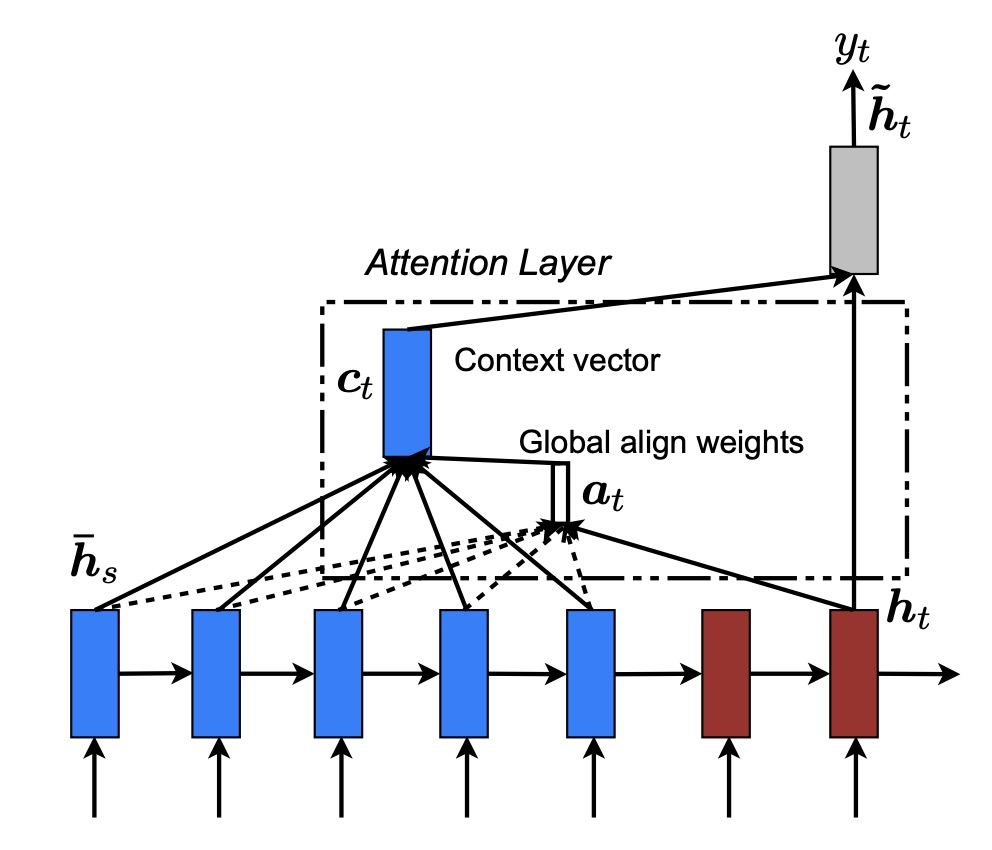A sequence-to-sequence RNN with global (Luong) attention, Luong, Pham & Manning “Effective Approaches to Attention-based Neural Machine Translation,” EMNLP 2015
In the diagram above we see sequence-to-sequence RNN with global (Luong) attention. The bottom row shows encoder hidden states $ \bar h_{1}, \bar h_{2}, \dots, \bar h_{S}$ in blue, feeding into the decoder’s hidden state $h_{t}$ (red). From each encoder state, arrows (dashed for lower weights, solid for higher) converge onto the context vector $c_{t}$ in the attention layer. The context vector (blue vertical block) is then concatenated with the decoder’s current hidden state (dark gray block) to produce the combined output vector $\tilde h_{t}$, from which the next token $y_{t}$ is generated
Scaled Dot-Product & Multi-Head Attention
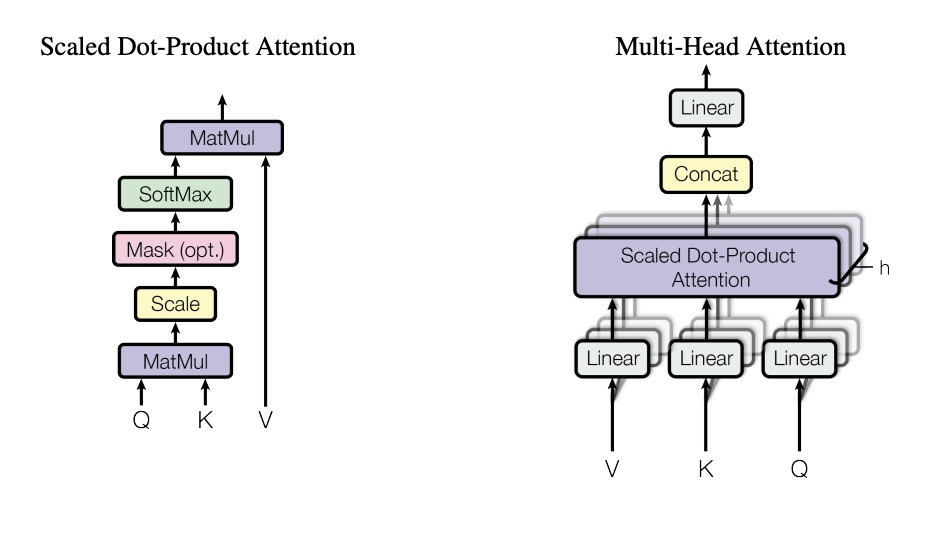
Vaswani et al. (2017) introduced scaled dot-product attention and multi-head attention in the Transformer:
\[\mathrm{Attention}(Q,K,V) = \mathrm{softmax}\!\Bigl(\tfrac{Q\,K^\top}{\sqrt{d_k}}\Bigr)\,V\]Here, $Q$, $K$, and $V$ are the query, key, and value matrices obtained by linear projections of the inputs. Scaling by $\sqrt{d_k}$ prevents dot-products from growing too large in high dimensions, stabilizing gradients (arxiv.org, nlp.stanford.edu).
Multi-head attention runs this computation in parallel $h$ times with different projection matrices:
\[\mathrm{head}_i = \mathrm{Attention}(Q\,W_i^Q,\,K\,W_i^K,\,V\,W_i^V), \quad \mathrm{MultiHead} = \bigl[\mathrm{head}_1; \dots; \mathrm{head}_h\bigr]\,W^O\]This allows each head to capture different relationships (e.g., syntactic vs. semantic) simultaneously (arxiv.org).
Multi-head attention block from “Attention Is All You Need”
A Taxonomy of Attention Variants
Global vs. Local:
- Global attends over all encoder positions every step (Luong’s global)
- Local restricts attention to a sliding window (Luong’s local), trading off speed vs. context (arxiv.org).
Self-attention vs. Cross-attention:
- Self-attention computes $Q,K,V$ from the same sequence (e.g., within an encoder or decoder layer), enabling context mixing as in Transformers (en.wikipedia.org).
- Cross-attention matches decoder queries to encoder keys/values.
Content-based vs. Positional:
- Content-based scores purely on vector similarity (Bahdanau, Luong).
- Positional incorporates absolute or relative position embeddings, crucial in non-recurrent architectures (en.wikipedia.org).
Key–Value attention:
- Distinguishes between keys (used for scoring) and values (used for context), as formalized in QKV attention.
Sparse / Adaptive / Structured attention:
- Variants that enforce sparsity (e.g., hard attention), dynamic spans, or graph-structured weights for efficiency and interpretability (en.wikipedia.org).
Domain-specific flavours:
- Spatial vs. Channel attention in vision (e.g., SENets), graph attention in GNNs, memory-augmented attention in reinforcement learning, etc.
Applications Beyond Translation
Since their NMT debut, attention mechanisms have propelled advances across modalities:
- Summarization & Question Answering: Focus on key sentences or document passages.
- Image Captioning & Vision: Spatial attention over image patches (e.g., “Show, Attend, and Tell”).
- Speech Recognition: Soft-alignment between audio frames and output characters (researchgate.net, arxiv.org).
- Reinforcement Learning & Memory: Neural Turing Machines and Memory Networks use attention as read/write controllers (medium.com).
Practical Tips & Implementation
Complexity & Memory:
- Vanilla attention is $O(n^2)$ in sequence length.
- Use local or sparse variants for very long inputs.
Libraries & Snippets:
- TensorFlow/Keras:
tf.keras.layers.Attention,MultiHeadAttention - PyTorch:
torch.nn.MultiheadAttention
- TensorFlow/Keras:
Visualization:
- Plot heatmaps of attention weights to interpret model focus (e.g., in NMT or QA).
Emerging Directions
- Efficient Attention: Linformer, Performer, Longformer replace full softmax with low-rank, kernelized, or sliding-window schemes.
- Hybrid Architectures: Combining recurrence/convolution with self-attention for best of both worlds.
Interpretability & Fairness:
- Investigating whether attention truly explains model decisions, and adapting it to debias outputs.
Conclusion
Attention mechanisms—from Bahdanau’s additive form to Vaswani’s multi-head—have reshaped neural architectures by providing dynamic, interpretable connections between inputs and outputs. As research pushes toward ever more efficient, specialized, and transparent attention variants, this family of techniques remains central to the evolution of deep learning.