A Gentle Introduction to Vector Projection in Python with NumPy
Vector projection is a fundamental concept in linear algebra that often appears in machine learning, computer graphics, and physics simulations. By projecting one vector onto another, you find the component of the first vector in the direction of the second. In this blog post, you’ll learn what vector projection is, why it matters, and how to implement it in Python using NumPy.
What Is Vector Projection?
Given two vectors \(\mathbf{a}\) and \(\mathbf{b}\), the projection of \(\mathbf{a}\) onto \(\mathbf{b}\) (sometimes called the “scalar projection” times \(\mathbf{b}\)) is:
\(\text{proj}_{\mathbf{b}}(\mathbf{a}) = \left( \frac{\mathbf{a} \cdot \mathbf{b}}{\|\mathbf{b}\|^2} \right) \mathbf{b}.\)
\(\mathbf{a} \cdot \mathbf{b}\) is the dot product of vectors \(\mathbf{a}\) and \(\mathbf{b}\).
\(\|\mathbf{b}\|^2 = \mathbf{b} \cdot \mathbf{b}\) is the **square** of the magnitude of \(\mathbf{b}\).
In simpler terms, \(\mathbf{a} \cdot \mathbf{b}\) tells us how “aligned” \(\mathbf{a}\) is with \(\mathbf{b}\). Dividing by \(\|\mathbf{b}\|^2\) scales this alignment relative to the length of \(\mathbf{b}\). Finally, multiplying by \(\mathbf{b}\) orients the resulting vector along the direction of \(\mathbf{b}\).
Why Does Vector Projection Matter?
- Machine Learning: Projection can be used to reduce dimensionality or to remove unwanted components from data (e.g., subtracting out a particular direction in a dataset).
- Computer Graphics: In 3D engines, projections are used to find how a point or a force vector aligns with a particular surface or direction.
- Physics Simulations: You often need to decompose forces into components along certain axes or directions.
Setting Up Your Python Environment
To follow along, you’ll need Python and the NumPy library installed. If you don’t have NumPy, install it via:
1
pip install numpy
Then, import it in your Python script or Jupyter notebook:
1
import numpy as np
Implementing Vector Projection in Python
Below is a simple function that computes the projection of a vector (\mathbf{a}) onto another vector (\mathbf{b}):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import numpy as np
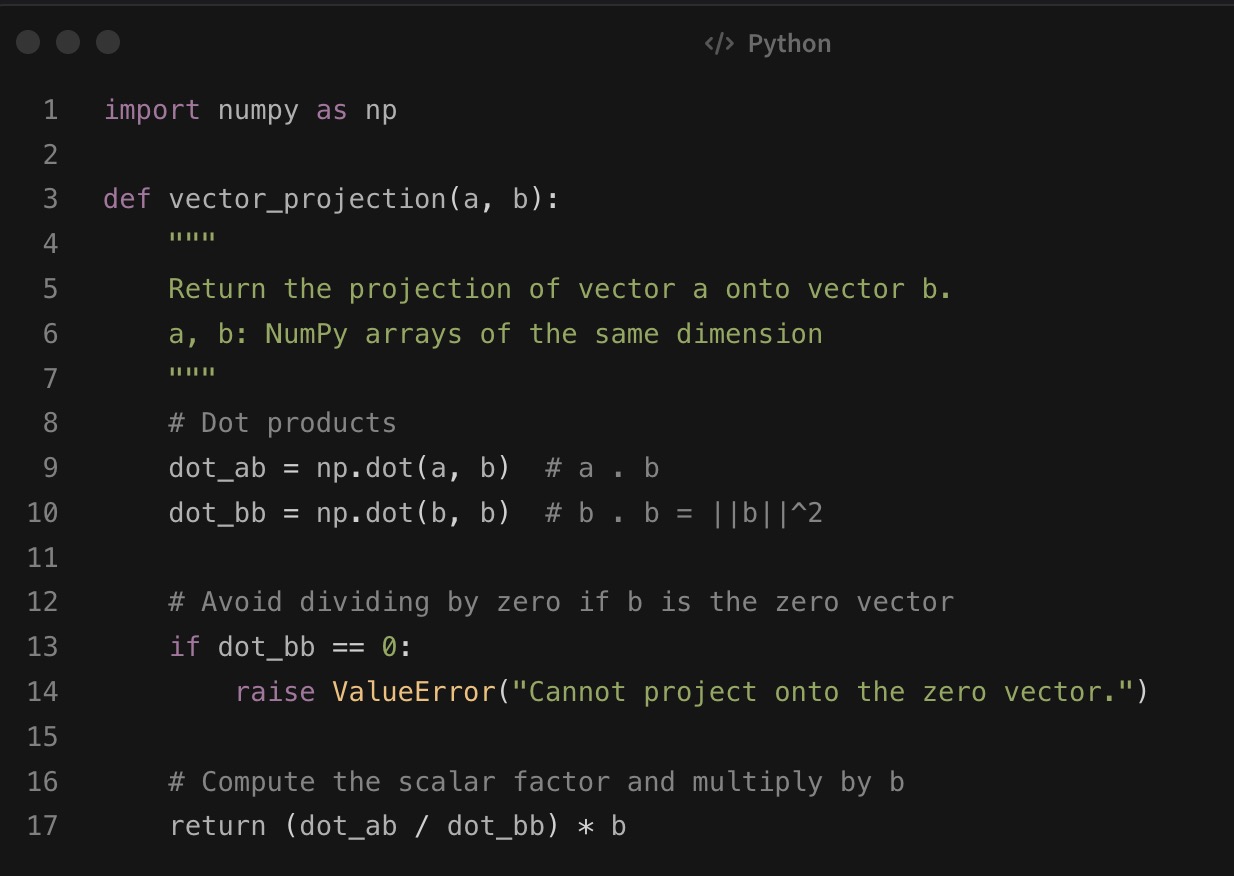
def vector_projection(a, b):
"""
Return the projection of vector a onto vector b.
a, b: NumPy arrays of the same dimension
"""
# Dot products
dot_ab = np.dot(a, b) # a . b
dot_bb = np.dot(b, b) # b . b = ||b||^2
# Avoid dividing by zero if b is the zero vector
if dot_bb == 0:
raise ValueError("Cannot project onto the zero vector.")
# Compute the scalar factor and multiply by b
return (dot_ab / dot_bb) * b
Step-by-Step Explanation
1. Dot Products: We use `np.dot(a, b)` to compute \(\mathbf{a} \cdot \mathbf{b}\) and `np.dot(b, b)` to compute \(\|\mathbf{b}\|^2\). 2. Zero Vector Check: If \(\|\mathbf{b}\|^2 = 0\), then \(\mathbf{b}\) is a zero vector and we can’t project onto it. 3. Projection: Multiply \(\mathbf{b}\) by the scalar \(\frac{\mathbf{a} \cdot \mathbf{b}}{\|\mathbf{b}\|^2}\).
Trying It Out
Let’s test this function with a quick example:
1
2
3
4
5
6
7
if __name__ == "__main__":
# Example vectors in 2D
a = np.array([3, 4])
b = np.array([-2, 4])
proj_ab = vector_projection(a, b)
print("Projection of a onto b:", proj_ab)
When you run this script, you should see something like:
1
Projection of a onto b: [-1. 2.]
This result corresponds to the component of \(\mathbf{a}\) in the direction of \(\mathbf{b}\).
Extending to Higher Dimensions
The same function works for vectors of any dimension, as long as they have the same length. For example:
1
2
3
4
5
a_3d = np.array([1, 2, 3])
b_3d = np.array([4, 0, 1])
proj_3d = vector_projection(a_3d, b_3d)
print("Projection of a_3d onto b_3d:", proj_3d)
The concept remains the same: we calculate dot products and then scale.
Integration with Pandas or ML Libraries
If your data is stored in a Pandas DataFrame, you can still perform vector projections by converting rows (or columns) to NumPy arrays:
1
2
3
4
5
6
7
8
9
10
11
12
13
import pandas as pd
# Suppose you have a DataFrame with columns x and y
df = pd.DataFrame({
'x': [3, -2],
'y': [4, 4]
}, index=['a', 'b'])
a_pd = df.loc['a'].values # array([3, 4])
b_pd = df.loc['b'].values # array([-2, 4])
proj_pd = vector_projection(a_pd, b_pd)
print("Projection of a_pd onto b_pd:", proj_pd)
Scikit-learn or other ML libraries typically rely on NumPy arrays for underlying computations, so you can easily integrate the vector_projection function into your machine learning pipelines if you need custom vector math.
Conclusion
Vector projection is a straightforward yet powerful linear algebra operation that pops up in numerous scientific and engineering fields. By using NumPy’s efficient dot product functions, you can implement vector projections in just a few lines of Python. This makes it easy to incorporate projection into your data analysis, machine learning, or physics simulations.
Feel free to experiment with higher-dimensional vectors or integrate this function into your existing data workflow. Once you understand the basics of vector projection, you’ll find it an invaluable tool for dissecting and interpreting vector relationships in all kinds of applications.
Happy coding! If you have any questions or would like to share your projects involving vector projection, let me know in the comments below.